Introduction to the Event Study Methodology
Finance theory suggests that capital markets reflect all available information about firms in the firms' stock prices. Following this premise, one can study how a particular event changes a firm's prospects by quantifying the impact of the event on the firm's stock. Finance scholars have developed the event study methodology to perform this type of analysis - in its most common form, with a focus on stock returns, in less used forms, with a focus on trading volumes and volatilities.
Return event studies quantify an event's economic impact in so-called abnormal returns. Abnormal returns are calculated by deducting the returns that would have been realized if the analyzed event had not taken place (normal returns) from the actual returns of the stocks. While the actual returns can be empirically observed, the normal returns need to be estimated. For this, the event study methodology makes use of expected return models, which are also common to other areas of Finance research.
The market model is the most frequently used expected return model in event studies. It builds on the actual returns of a reference market and the correlation of the firm's stock with the reference market. Equation (1) describes the model formally. The abnormal return on a distinct day within the event window represents the difference between the actual stock return ($R_{i,t}$) on that day and the normal return, which is predicted based on two inputs; the typical relationship between the firm's stock and its reference index (expressed by the $\alpha$ and $\beta$ parameters), and the actual reference market's return ($R_{m,t}$).
$$AR_{i,t}=R_{i,t}-(\alpha_i+\beta_i R_{m,t}) (1)$$
Such an analysis performed for multiple events of the same event type (i.e., a sample study) may yield typical stock market response patterns, which have been at the center of prior academic research. Typical abnormal returns associated with a distinct point of time before or after the event day are defined as follows.
$$AAR= \frac{1}{N} \sum\limits_{i=1}^{N}AR_{i,t} (2)$$
To measure the total impact of an event over a particular period (termed the event window), one can add up individual abnormal returns to create a cumulative abnormal return. Equation (2) formally shows this practice. The most common event window found in studies is a three-day event window starting at $t_1=-1$ and ending at $t_2=1$.
$$CAR(t_1,t_2)=\sum\limits_{t=t_1}^{t_2} AR_{i,t} (3)$$
Figure 1 plots the CAR values of two different corporate event types, FDA approvals, and the issuance of special dividends as they change when the event window is gradually extended. The figure suggests that the capital market perceives both event types as good news.
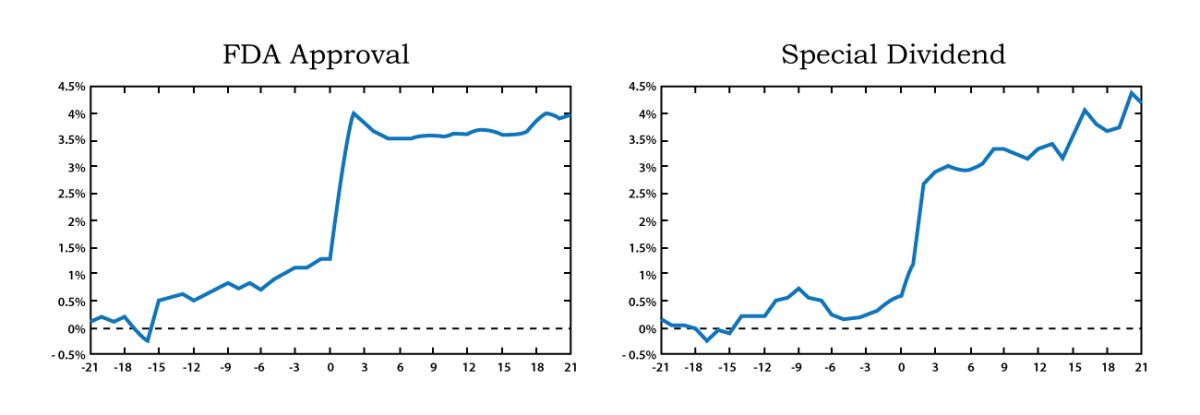
Source: Adapted from Neuhierl et al. (2011: 48)
In a sample event study that holds multiple observations of individual event types (e.g., acquisitions), one can further calculate cumulative average abnormal returns (CAARs), which represent the mean values of identical events. Equation 3 shows the formal equation for CAARs and Figure 2 illustrates CAARs and their standard deviations in the example of a ten-year study in the global insurance industry (Schimmer, 2012). The presented CAARs represent the average stock market responses (in percent) to press releases describing different types of corporate decisions.
$$CAAR= \frac{1}{n} \sum\limits_{i=1}^{n}CAR(t_1,t_2) (4)$$
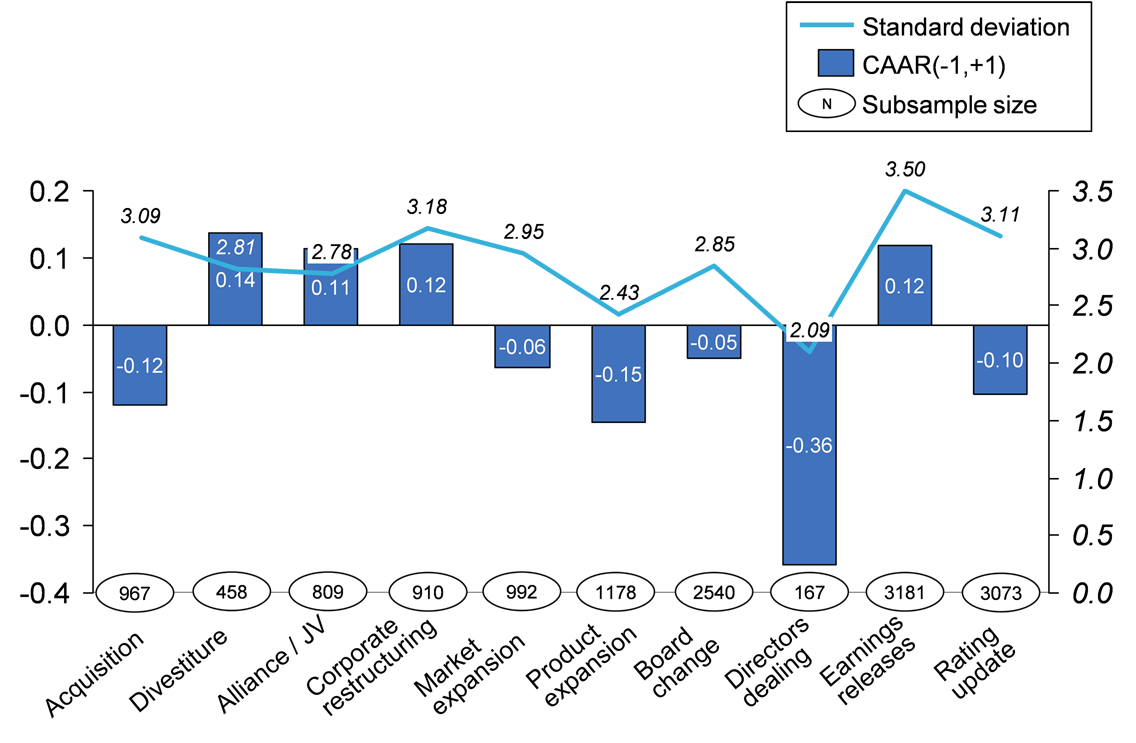
Source: Own Illustration
In addition to the above-presented introduction to the event study methodology, you may find the subsequent third-party video on YouTube helpful.
References and additional links
Neuhierl, A., Scherbina, A. and Schlusche, B. 2011. 'Market reaction to corporate press releases'. Available at SSRN: http://ssrn.com/abstract=1556532.
Schimmer, M. 2012. Competitive dynamics in the global insurance industry: Strategic groups, competitive moves, and firm performance. Wiesbaden: SpringerGabler.
